Optimal Deployment of Dynamic Wireless Charging for Battery Electric Vehicle
This blog talks about the research “Optimal asset management strategies for mixed transit fleet” published in the Transportation Research Part D: Transport and Environment in this link: https://doi.org/10.1016/j.trd.2020.102385
Keywords: Bi-level Formulation, Radial Basis Function, User Equilibrium, Dynamic Wireless Charging, Algorithm Design.
1. Introduction
The transportation sector is the top three causes of global warming and countries across the world are making effort and regulating greenhouse gas emission (GHG). A significant share of GHG comes from internal combustion engine vehicles (ICEV) or simply gas car since it burns fossil fuel and emits GHG during the process. Battery electric vehicle (BEV) presents as a solution to this problem because it emits little to no GHG, but it has two disadvantages compare to ICEV which are (1) considerably less driving range and (2) extensive charging time. An ICEV can have on average 460 miles of driving range and can be fueled to full by as soon as 3 minutes whereas these numbers for BEV are 250 miles and 30 minutes, which only applies for supercharger station.
To resolve these problems, Dynamic Wireless Charging (DWC) is invented, and this technology is evolving in efficiency. DWC can be implemented under a road, and it will dynamically charge BEVs as they drive above it. This poses a question for the city planners and local government on how and where to deploy these DWC. Therefore, the objective of this research is to develop a planning framework to optimally locate DWC facility considering both the system level network cost and driver’s new travel pattern due to DWC deployment.
2. Methodology
The problem is actually more complex since there are two entities with different interest involved in the final outcome of the DWC deployment. The local government will decide on the DWC plan, which is how much to invest and where to locate these facilities across the road network. This is referred to as the upper level. The upper level’s decision variable is the DWC plan, and its objective is to minimize the total system travel time. It might be tempting to implement DWC on road segment with higher traffic flow since it can provide more charging to more people. However, the BEV drivers will respond to this DWC plan and choose their routes that not only minimize travel time but also maximizie energy recharge and this process is referred to as lower-level. Therefore, high traffic flow will attract more BEV drivers and creates congestion which is not ideal. In addition, driver is also aware of other’s decisions. In classic traffic flow modeling, there exists an Wardrop User Equilibrium state where: “for every driver, the path travel times in all routes actually used are equal or less than those that can be chosen, and no drivers can unilaterally improve their travel time by switching route”. The dynamic between these two levels regarding to their objective and decision variables are shown in the figure below:
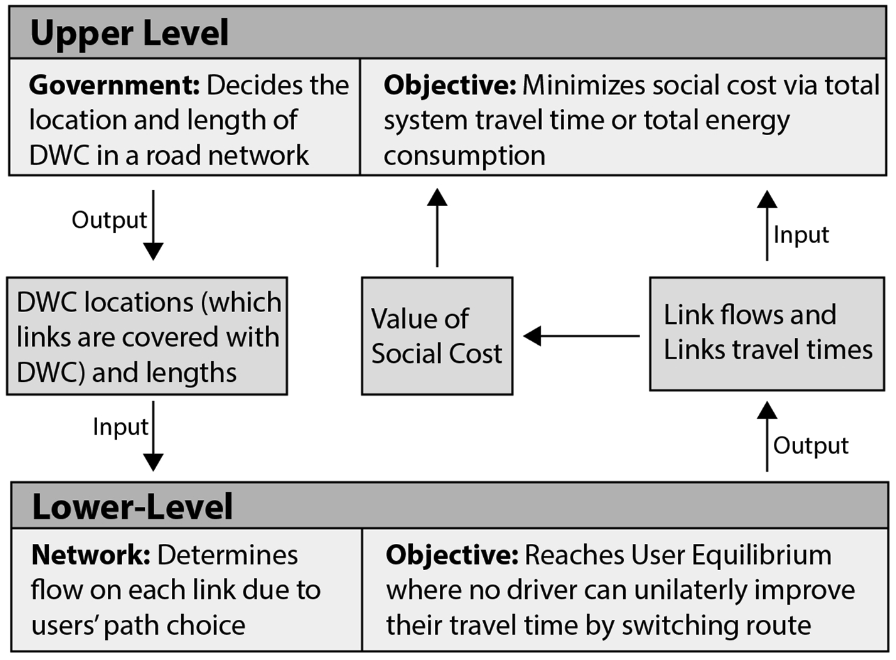
Figure 1. Interaction between the upper and lower level
Therefore, this problem can only be formulated as a bi-level optimization problem with an expensive objective function. For the solution algorithm, the author takes inspiration from genetic algorithm in conjunction with the Radial Basis Function Interpolation to accelerate the convergence time. The framework is scripted and coded in MATLAB and General Algebraic Modeling System (GAMS). Readers interested more methodology can view the research paper at: https://doi.org/10.1016/j.trd.2020.102385
3. Conclusion
The framework is first tested on a 18 links network and then in a real-world case study of Montgomery County, Maryland, which has upwards of 4,420 links, 1,752 nodes, and peak hour demand of 3.5 million vehicles. Figure 2 and 3 show the application of the framework on these two networks. In the 18 links network, DWC implemented are colored in green and its thickness represents the DWC’s length as a percentage of the length of the link. For Montgomery country, the color is orange. One common observation is that the model does not aim to maximize DWC on any particular link but rather opts for a more spread-out approach. This is to prevent attracting drivers to certain part of the network creating unneccesary congestion.

Figure 2. DWC plan for the 18-link network
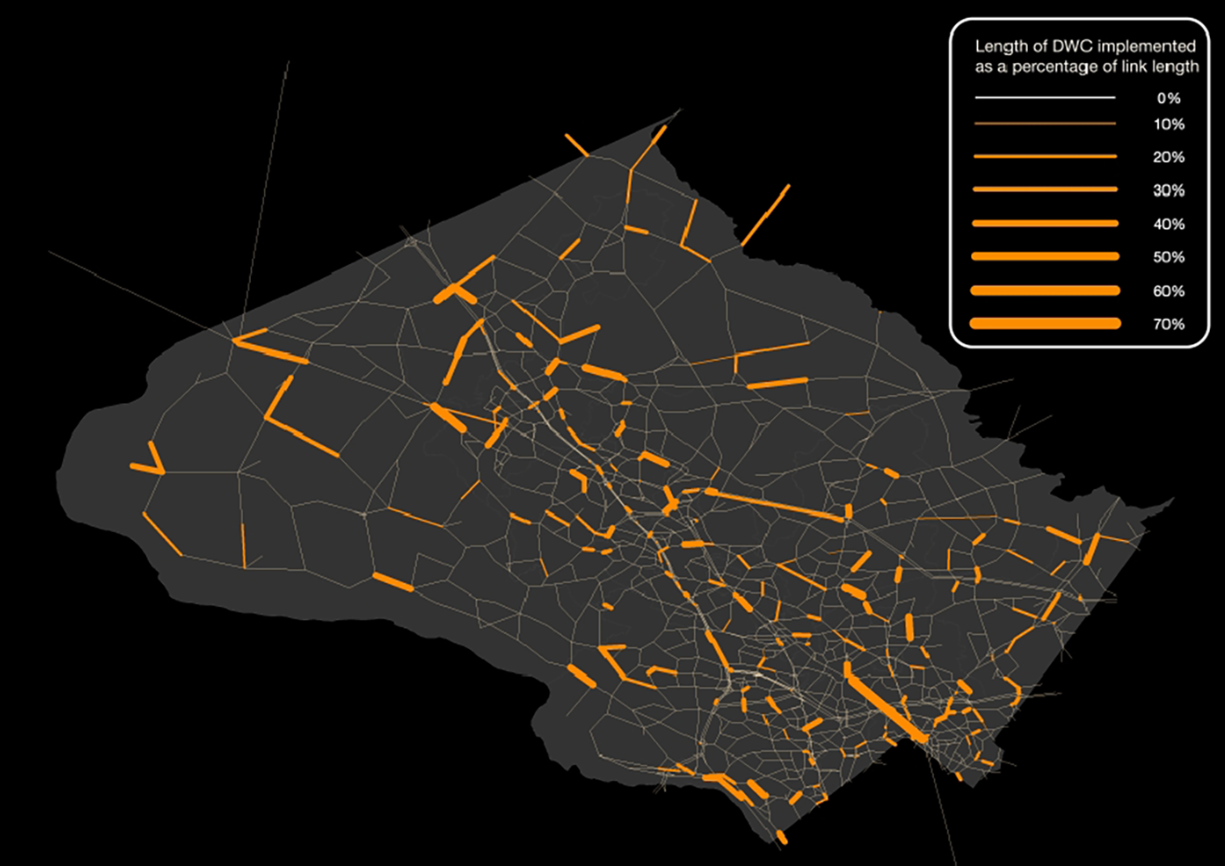
Figure 3. DWC plan for the Montgomery County Network
Author's Contribution in this project
The study concept and methodology are developed by all authors listed in the paper. This article author coded the methodology, conducted both case study applications, and wrote the majority of the paper.