Dispatching and Repositioning Autonomous Taxi Using Reinforcement Learning
This blog is based on a conference poster and presentation at the 101st Transportation Research Board Annual Meeting. Please see the additional resource section for the poster and presentation.
Keywords: Reinforcement Learning, A3C, Policy Function, Autonomous Taxi, Minimum-vertex Disjoint Path Cover
1. Introduction
Transportation Network Companies (TNC) is leveraging technology and connectivity to provide a more efficient taxi service with example such as Uber and Lyft. However, the system performance is still hindered by the spatial and temporal imbalance between supply and demand. TNC employs economic incentives such as surge pricing but only to limited success. Surge pricing has been shown to have relative weak impact on driver’s decision on accepting trip far away but siginificant impact on riders to cancel their trips. The surged price is also likely to be at an equilbrium higher than that of the efficient level. This can be addressed by introducing autonomous electric taxi (AET) into the system and repositioning these AET to balance supply and demand. This strategy can also work even if TNC still have human-driven vehicles (HV) where their objectives are considered. In addition, customer’s equity, where those with higher waiting time are prioritized, are also considered. Therefore, the objective of this research is to “develop a framework to optimally dispatch both HV and AET, reposition, and recharge AET with the objective of minimizing the customer wait time, cancellation penalty, and AET’s operational cost”.
2. Methodology
Environment Setting This research uses a centralized approach where the main controller will make every decision for all taxi whether it is single pickup, carpooling, repositioning, recharging, or idling. The spatial setup is a road network modeled as a graph where the vertices are intersections and edges are road segment connecting these vertices. The framework assumes the taxi request’s pickup and dropoff point is at these nodes though simple adjustment can be made if these points happen to be in the middle of the edge. In temporal setup, a continuous period (i.e., 6AM to 8PM) will constitues an episode and this episode is discretized into intervals, or time period, of equal duration (i.e., 5 minutes). Therefore, an episode can be described as T = [t1, t2, t3... tn]. The model is dynamic and stochastic where only the current taxi demand is known.
Framework Architecture At the start of the episode, AETs and HVs vehicle location and status and taxi demands are gathered. The framework employs 4 processes to model the decision making of the central controller. Process 1 aims to match taxi demand with current idling AETs and HVs. Customer’s wait time and HV’s time on the system are considered in the formulation. If there are unserved demand, Process 2 will match demand with single pickup AET for carpooling. If there are still unserved demand, Process 3 will match idling AET in zones nearby with demand. This is to mitigate the event where demand and taxi are very close to each other but cannot be matched from Process 1 due to different zones. For the remaining idling AET if any, Process 4 will decide on repositioning and recharging. The AET, HV, and taxi demand information are then updated and transferred to the next time period. The process is repeated until the end of the episode.
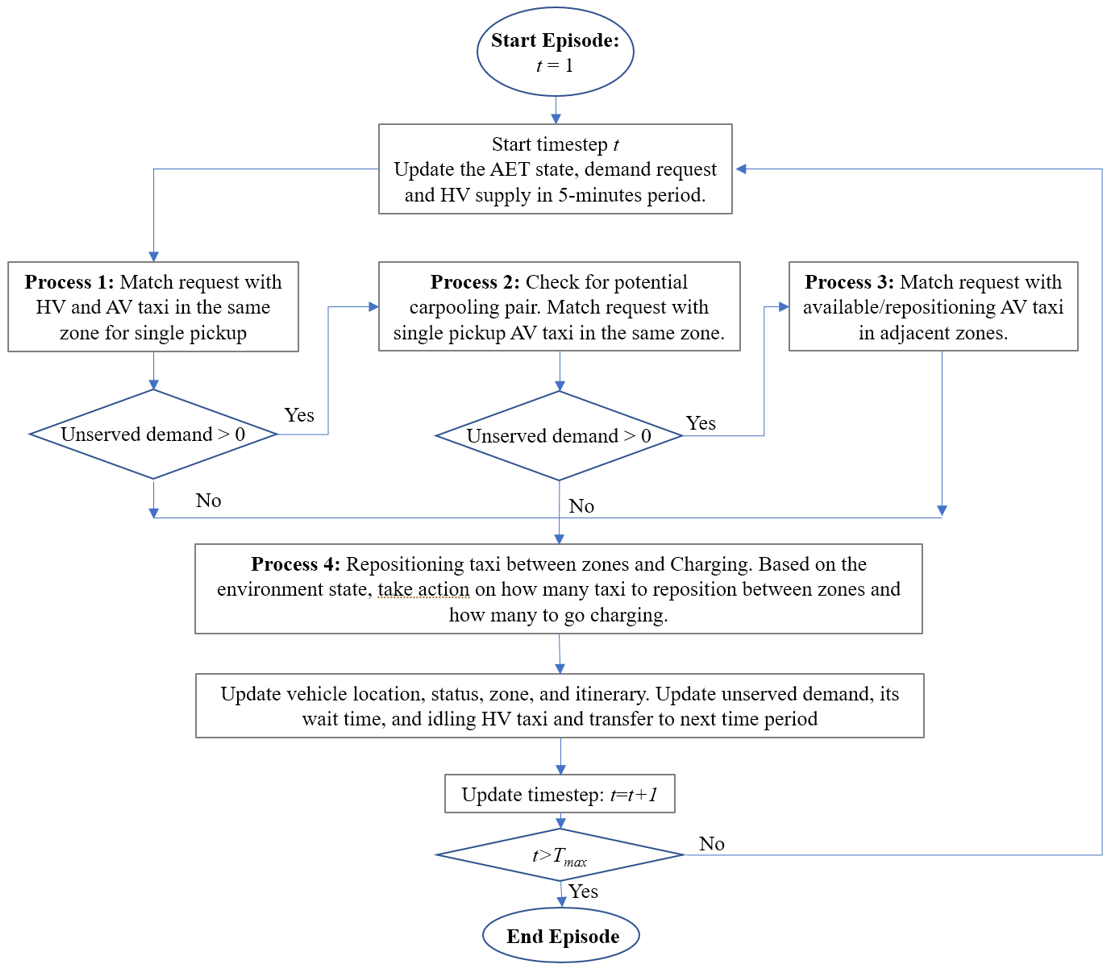
Figure 1. Framework Architecture
Process 1,2, and 3 are formulated as a mixed integer linear programming model whereas Process 4 uses reinforcement learning (RL). Reinforcement learning is an area in Machine Learning where given an environment state, an agent (i.e., the controller) will take an action, receive a reward, and the environment state is updated. Figure 2 shows an illustration of this process:
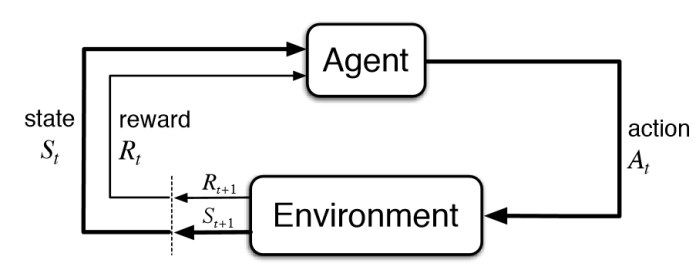
Figure 2. Illustration of Reinforcement Learning
In our case, the environment state includes unserved taxi demand, number of idling AET, future available vehicles, historical demand, and number of undercharged AET. Based on this information, the agent decides how many taxi to reposition from a zone to another considering all possibilities and how many to recharge at each zone. In classic RL literature, the agent is maximizing the reward thus in our case we introduce negative cost in place of reward. The negative cost is the negative of the sum between customer wait time, cancellation penalty, repositioning cost, and undercharged AET penalty. The agent trains by playing the episode multiple times and gathers the experience in form of a tuple representing what action is taken at what state and how much reward is collected.
3. Case Study and Preliminary Results
The Framework is demonstrated on the Anaheim, California road network. The taxi demand is simulated and the TNC is managing a fleet of 250 AVs on top of HV supply drawn from a historical distribution. We introduce the Manual Allocation Model as a baseline to compare with our framework. In Manual Allocation, AV will serve the nearest customer and there is no repositioning. We then pick a taxi from Manual Allocation and our framework respectively and compare their actions throughout the day or "A Day in the Life". Figure 3 shows the trajectory of these 2 taxis and Figure 4 shows the activities by time of the day. Activities are color-coded where single-pickup, carpooling, and repositioning are colored green, red, and blue respectively.
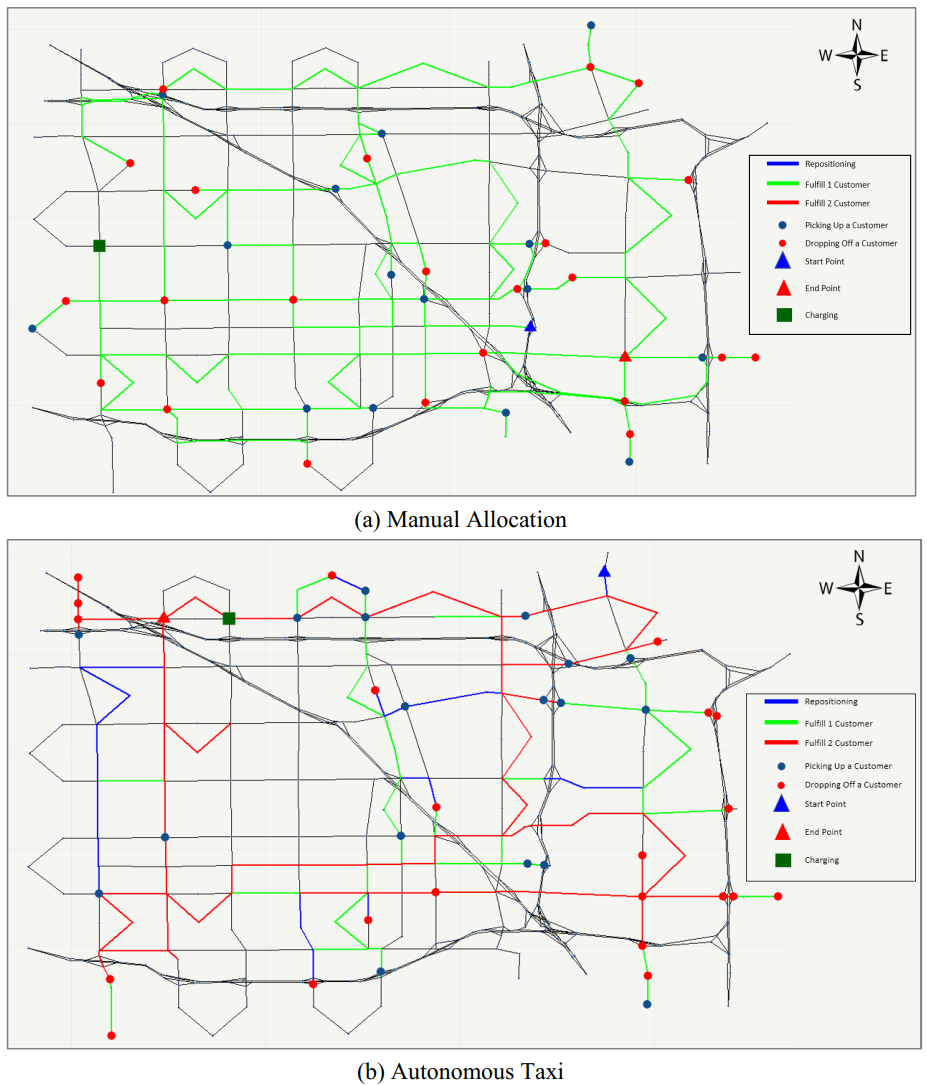
Figure 3. Taxi Trajectory throught the day
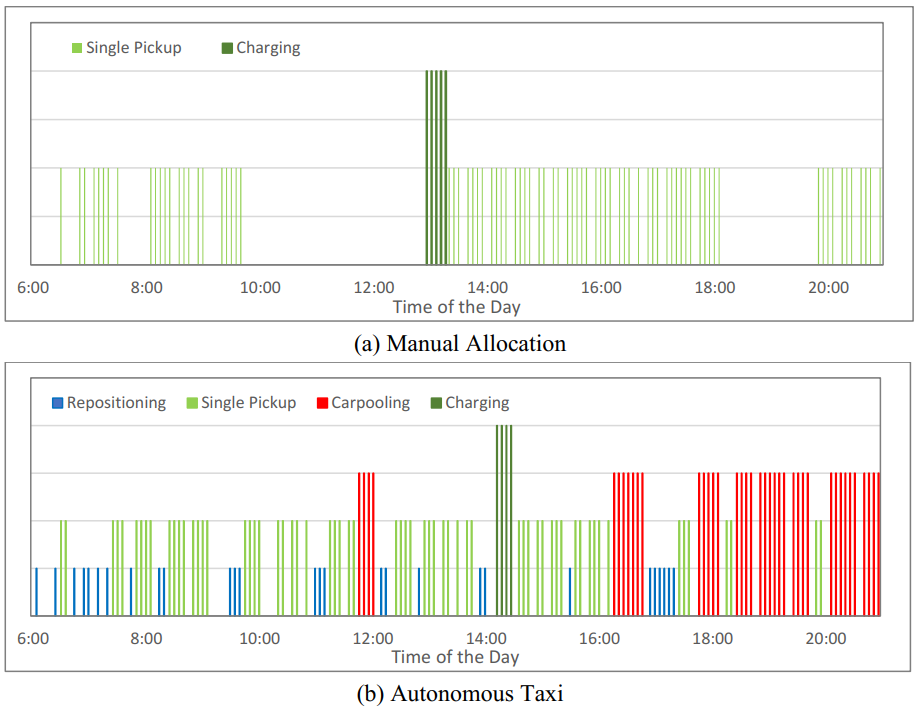
Figure 4. Taxi Activities
Author's Contribution in this project
The author is responsible for the problem concept, methodology, modeling in software, and writing of the paper. Optimization processes in single-pickup and carpooling are coded using the General Algebraic Modeling System whereas the Reinforcement Learning model are coded in python script. Due to the complex formulation, the script does not make use of exisiting RL library such as open ai gym, but it is still built on the framework of Pytorch. Figures are plotted using ggplot2 package from R language.